Ends Jan 8, 2026.

By Lawrence G. McMillan
This article was originally published in The Option Strategist Newsletter Volume 2, No. 13 on July 8, 1993.
Two strategies are equivalent when they have the same profit potential. That is, their profit graphs have the same shape. More experienced option traders know that an understanding of equivalent strategies or positions is vital. It can help in many ways. For example, one may be able to more effectively use his capital by establishing the more favorable equivalent strategy. Or, when trading, he may be able to get a better execution. Finally, he may be able to make better adjustments to his positions by using equivalent strategies. The concept is not new, but even a veteran trader may have to sort through some equivalences in order to choose the best position.
Example: The purchase of a call option is equivalent to the simultaneous purchase of common stock and the purchase of a put option. Both strategies have profit graphs with the same shape (see graph, right). There is unlimited upside profit potential and there is limited risk.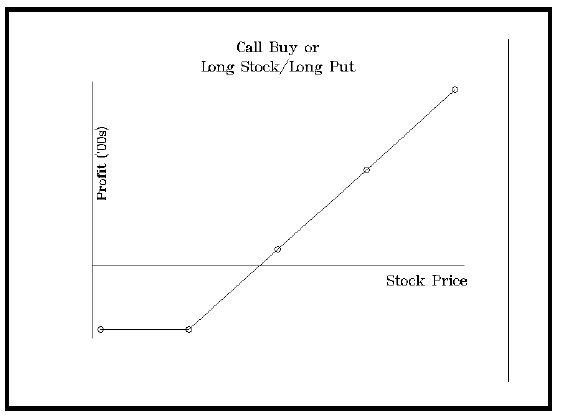
Determining Equivalences
Many option traders, short of memorizing a table of equivalences, may have trouble at first determining just what is equivalent to what. The following simple process may help.
First, assign a pair of numbers to each simple position; the first of the pair of numbers shows how the position does for each point that the underlying security rises above the striking price in question, while the second of the pair corresponds to how the position fares for each point that the underlying falls below the strike. For example, long stock would have the pair (+1,-1) associated with it — for each point that the stock rises above the strike, you make +1 point, while for each point that it falls below the strike, you make -1 points (i.e., you lose a point). The simplest strategies would have the following pairs:
Long stock = (+1,–1) Short Stock = (–1,+1) Long call = (+1,0) Short Call = (-1,0) Long put = (0,+1) Short Put = (0,-1)
Note that calls and puts have a zero as one number of the pair. For example a long call's pair is (+1,0) to demonstrate that it makes a point for each point that the underlying is above the strike, but it neither gains nor loses any points as the underlying falls below the striking price. In reality, what these pairs are describing is the shape of the profit graph: +1 means the graph is rising, 0 means it is flat, and –1 means it is falling.
One can use these pairs to determine equivalency by combining the pairs in the following manner: add the first number of the pair for all components of a strategy, and then separately add all the second numbers of each pair. This would create a new pair for the overall strategy. If the resultant pair is the same as another strategy's pair, then they are equivalent. For anyone familiar with vector addition in algebra, this works the same way.
Example: Let's use this method to show that long call is equivalent to long put combined with
long stock.
Long stock = (+1,–1)
Long put = ( 0,+1)
Combined position = (+1, 0)
We arrive at the pair for the "combined position" by initially adding the first number of each component: +1 for long stock plus 0 for long put. This gives us +1 as the first number of the pair for the "combined position". Now the second number for the combined position is determined by adding the second number for long stock (–1) to the second number for long put (+1). This gives us 0 as the second number of the pair for the combined position.
Now this "combined position" is equivalent to every other position that has a pair of (+1,0). In fact, a long call has exactly this pair. So this method has proven that a long call is equivalent to long stock combined with a long put.
You may think this is a rather arduous way to prove something that you may already know. However, it is the groundwork for determining many other equivalences. By using this simple method, you can quickly construct many equivalent strategies. Some, but not all, are listed below. Check them for yourself if you do not readily see that they are equivalent. Of course, futures traders may substitute "future" wherever "stock" is used in these examples.
Strategy Pair Equivalent Strategy Long call (+1,0) Long underlying + long put Long put (0,+1) Short underlying + long call Long stock (+1,-1) Long call + short put Short stock (-1,+1) Long put + short call Short call (-1,0) Short underlying + short put Short put (0,-1) Long underlying + short call = covered write Ratio write (-1,-1) Short straddle (long underlying + short two calls) or short underlying + short two puts
Rates of Return
Note that just because two strategies are equivalent, it does not mean that they have the same rate of return. For example, the risk is 100% when buying a call, whereas the risk of buying stock and buying a put (assuming the purchase is made on cash, not margin) would be considerably smaller percentagewise. A few issues ago, we compared the equivalent strategies of covered writing versus selling naked puts. Now these two strategies seem to be at opposite ends of the spectrum: many conservative investors think nothing wrong with doing covered call writes, but would never consider selling a naked option. In reality, they are equivalent strategies (limited profit potential coupled with downside risk). In fact, the margin requirements are more favorable for selling naked puts so that it may often prove to be the superior strategy to covered call writing (see volume 2, no. 9 issue for more details).
Better Executions
At times, it may be advantageous to use an equivalent strategy to cut down on cost of executions of in-the-money options — not commissions, but on the bid-asked spread differential. This is often true for futures options. Rather than buying the in-the-money option — which may have a wide spread between the bid and offer — it may be more advantageous to use an out-of-the-money option (with a smaller spread between the bid price and asked price) combined with the underlying security. The out-of-the-money option may have more open interest and therefore have a "tighter" market for trading.
Example: Pork Bellies are trading at 38 cents, and a trader wants to short them. But, being leery of the volatility of bellies, he wants to buy August 45 puts instead. Unfortunately, the puts are quoted as 6.50 bid and 7.50 offered. Thus, he has to pay a premium of 0.50 to the last sale (38 + 7.50 - 45 = 0.50) in order to buy the puts. This is an unreasonable price since the put should be trading near parity. However, the equivalent position to a long put is "short futures, long call". He sees that the August 45 call is trading at 0.10 bid, offered at 0.20. Now, if he were to buy the call at 0.20 and sell the futures short at 38, he would only be paying a time premium of 0.20 for the equivalent position.
Using this strategy with futures, one would not have to use much more margin for the equivalent position than would be needed to buy the put. However, with stocks, the extra investment would normally be prohibitive. Still, if one needs a short-term trade in a stock option, it may be more advantageous to use this "equivalence" strategy rather than pay an inordinate amount of time value premium for an in-the-money option.
Strategy Decisions
Knowing the equivalences may help one to clarify a strategy in his mind. For example, covered writing of out-of-the-money calls is equivalent to naked writing of in-the-money puts. When viewed in this light, it is obvious that writing out-of-the-money calls is a quite bullish strategy that has substantial downside risk and does not bring in a lot of time value premium.
Being aware of equivalent strategies is also important when adjusting positions, for it may well behoove one to use an equivalent strategy to limit his losses in a fast-moving market. For example, if one is short a straddle and the underlying makes a fast move to the downside, the puts that one is short may quickly become fairly deep in-the-money. If one is having trouble covering the puts — either because the markets are wide or because he can't get an accurate market — then he should consider using the equivalent strategy described above: short the underlying and buy the out-of-the-money call.
In a similar vein, the equivalent strategy can be used to illustrate the difference between covering a short option and merely hedging it with the underlying stock. In our short straddle or combination positions, we sometimes recommend that one take follow-up action by covering the short options if the underlying moves too far; at other times, we merely use the underlying security to hedge the short options. There is, of course, a major difference in the two strategies. Viewing equivalent positions will demonstrate just how much. First of all, if one covers an option that he is short, all further risk from that option is removed. However, if he merely hedges the short option with the underlying security, he creates another risk:
Example: One is short calls on XYZ and XYZ moves up through his mental stop point. Rather than pay the excess time premium involved to buy back the calls, he decides to buy stock instead. This effectively converts his short calls into short puts, so he still has risk if XYZ were to subsequently fall in price.
Original position: short call = (-1, 0) Adjustment: buy stock = (+1,-1) Resulting position: ( 0,-1) = short put
Thus by buying the stock, he has removed his upside risk, but he has introduced a downside risk. In simple terms, he is no longer short a call, but is now short a put.
No one likes to pay excess time value premium when he does not have to, so the best time to use stock as a hedge is when expiration is relatively close, and the stock therefore does not have a good chance of reversing direction and causing pain from a move in the other direction. Alternatively, if there is too much time left until expiration, then it is best to cover the short option (or to use the complete equivalent strategy as described in the previous section), rather than merely using the underlying security to hedge.
We have written before on one other use of equivalent strategies: using options to cover a futures position when futures are locked at the limit. We last wrote about it when lumber was moving limit up for days on end. Anyone who was short lumber would have been ruined had he not used options. With options, he could have limited his loss by "buying" futures with the equivalent option strategy: buy the calls and sell the puts, both with the same striking price. This is an important equivalence of which every futures trader should be aware, since it is his only means of taking his loss when futures are locked at the limit.
In summary, an option trader should be familiar with equivalent strategies for they are important in visualizing his strategies and are useful as alternatives in "thin" or fast markets.
This article was originally published in The Option Strategist Newsletter Volume 2, No. 13 on July 8, 1993.
© 2023 The Option Strategist | McMillan Analysis Corporation

