Portfolio Protection, Revisited (20:21)

By Lawrence G. McMillan

This article was originally published in The Option Strategist Newsletter Volume 20, No. 21 on November 17, 2011. 

We have written about the subject of protecting a portfolio of stocks with derivatives several times over the years, although it’s been a while (Volume 19, Numbers 6 and 12 had articles on the subject). Recently, some subscribers have inquired about how to calculate the amount of protection they need.

One facet of this calculation that seems to need some clarification is the work that one must do in order to convert his own portfolio net asset value into a net asset value that corresponds to a particular index within which one is considering buying protection. So, in this article, we’ll go over an example of how to do these calculations for a sample portfolio.

Many portfolio managers – even if they are merely managing their own portfolio – are concerned about protecting the gains of a bull market, or protecting against losses if a bear market should emerge. However, most portfolio managers are reluctant to give away the upside.

That is, they don’t want to move to a large cash position or to sell short against their position.

This is where derivatives strategies can be quite useful. One is able to buy “insurance” in case the market declines. The cost of such insurance can be adjusted to fit the needs of the individual portfolio manager.

There are many ways that a portfolio can be protected, without actually selling out the stocks. One can take a “macro” approach and use broad-based index options to hedge broad market risk (such as the S&P 500, the NASDAQ 100, or VIX). This approach is usually the most efficient in terms of cost, but might not meet one’s needs in other areas. For example, if the individual portfolio does not really track the S&P 500 very well, then a hedge using S&P 500 options may not work properly.

The “micro” approach is more work. It generally involves hedging individual stocks with options on each individual stock. This approach gives the best hedge, of course, since the hedging vehicles pertain exactly to the individual stocks and there is no tracking error. However, it can be quite costly, both in terms of “insurance dollars” and in terms of time spent managing the positions.

"Macro" Approaches

Those managers utilizing the “macro” approach feel that their portfolio resembles a major index average closely enough, so that futures or options on that index can be used to hedge the portfolio. Unless one is running an index fund, he is likely to have some tracking error between his actual portfolio and that of the index derivatives used as a hedge. However, in most cases, the portfolio manager does not mind a small tracking error, as long as he knows that the protection is in place, guarding against a swift or severe market decline.

“Macro” strategies involving broad-based derivatives include: buying index puts, buying index put spreads, selling index calls, collars, selling index futures, buying volatility futures, and buying volatility calls.

If establishing an $SPX hedge by buying index puts, one would buy enough puts to fully hedge the value of his portfolio at the striking price.

Example: suppose one has a portfolio that behaves exactly like $SPX. Moreover, the net asset value of his portfolio is $3 million. He decides to hedge by buying SPX June 1200 puts. Then he would buy this quantity:
Quantity = Portfolio Value / (100 x Strike)
= 3,000,000 / (100 x 1200)
= 25 puts
(This assumes that the options are worth $100 per point of movement; that’s where the 100 comes from in the formula).

Volatility-Adjusting the Portfolio Net Asset Value

Even if one has a portfolio that behaves “like” a certain broad market index, it is likely that the stock portfolio is either more volatile or less volatile than the index itself (more volatile, in most cases). Therefore, one cannot merely hedge the net asset value of his portfolio, for that would not be the proper hedge.

If one is intending to use $SPX derivatives for protection, but one’s portfolio does not exactly mirror $SPX, then he must adjust the portfolio to conform to $SPX before he buys the protection.

First, each stock in one’s portfolio should be volatility-adjusted in dollar terms. That is, the dollar value of each holding should be adjusted by its comparative volatility (some might say Beta). If one has stocks in his portfolio with negative Beta (for example, gold stocks), they should probably be excluded from the macro calculations. Here is an example:

Example: one has a small portfolio of three diverse stocks. He would like to hedge it with $SPX put options. The price of each stock is shown in Table 1. Its volatility is shown as well. Furthermore, the “adjusted volatility” is shown, which is merely the stock’s volatility divided by $SPX volatility, which is assumed to be 16% in this example. Typically, one would use the 20-day historical volatility of $SPX, unless it were unusually high or low at the current time, in which case a longer-term (100-day?) historical volatility could be used. One could substitute Beta for “adjusted volatility,” but Beta is such a long-term measure that it can give inaccurate hedging calculations. Finally, the dollar amount of each stock is multiplied by the ”adjusted volatility.” The sum of the adjusted volatilities is thus the gross dollar amount of SPX to hedge.

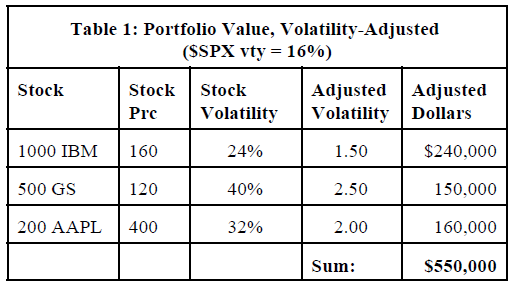
So, the total dollar value of this portfolio, adjusted for $SPX volatility, is the sum of the three numbers in the right-hand column of Table 1, or $550,000. Note that this is quite different from the actual net asset value of the three stocks, which is $300,000. In other words, these stocks are all more volatile than $SPX, so one needs to buy $550,000 worth of $SPX protection in order to hedge the $300,000 value of this small portfolio.

The number of puts to buy is:
   #of $SPX puts = (Volatility-adjusted value)/(100 x SPX Striking Price)

So, if one were going to buy $SPX puts with a striking price of 1100 to hedge this portfolio, he would buy (550,000)/(100*1100) = 5 puts.

Note: the 100 in the denominator of the formula is the trading unit of the puts; they are worth $100 per point of movement.

If one had a portfolio of technology stocks, he might want to use QQQ as the hedging index, rather than $SPX. The same steps as in the above example would apply, except that one would use the volatility of QQQ, not $SPX, when calculating the volatility-adjusted dollar value of each stock.

Protecting with $VIX Calls

In the past, we have often stated that we prefer using $VIX calls to hedge a portfolio, rather than $SPX puts. There are some caveats to that, of course. For example, $VIX may not rise even though $SPX falls – at least not over a short period of time. This happened in the first quarter of 2009, and is more susceptible to occurring when $VIX is already at a high level to begin with.

But if one does use $VIX calls as a hedge, he should use the $SPX volatility-adjusted portfolio value in the calculation of how many calls to buy. However, he does not need to hedge that full volatility-adjusted value, since $VIX is so volatile. Rather, we suggest hedging 20% of that value (a figure based on several independent studies done in recent years). Furthermore, he should use a $VIX strike that is three “full” strikes out of the money – where a “full” strike is 2.50 points when $VIX is below 30, and is 5.00 points when $VIX is above 30.

Example: suppose $VIX is trading at 25. The hedger decides to buy the VIX Dec 32.5 calls. Suppose he wants to hedge the portfolio shown in Table 1. Quantity = 20% * NAV / (100 * Strike price) = 20% * $550,000 / (100 * 32.5) = $110,000 / 3250 = 34 calls

There is a potential problem with the formula in the above example, though. It implies that, the higher the $VIX strike, the fewer calls one should buy. This may work out okay, for when $VIX is “too high,” it is likely that the stock market will rally soon thereafter, and perhaps not as much protection is needed. Conversely, when $VIX is very low, the danger of a market downturn is increased, so perhaps you should buy more calls.

Perhaps a better approach is to use a fixed quantity of $VIX calls to buy at all times – something on the order of: buy 7 $VIX calls, three “full strikes” out of the money, for each $100,000 of volatility-adjusted portfolio value that one wants to hedge, regardless of the actual level of $VIX. That would indicate 38 calls for the above example portfolio. The two methods will yield similar results except when $VIX is at extremely high or low prices.

If one has a portfolio that behaves like QQQ, there is no direct volatility call to hedge with (there are no listed options on $VXN – the NASDAQ “$VIX”). He can use $VIX calls, but there could be tracking error.

Summary

Buying $VIX calls or index puts for protection is a viable method of hedging a stock portfolio, while still leaving room for the portfolio to appreciate in price if the stocks in the portfolio rise. Thus, it is preferable to hedging with futures or selling index call options – both of which cut off the upside profit potential of the portfolio. One should be careful to hedge the volatility-adjusted value of his portfolio, and not merely the raw net asset value.

This article was originally published in The Option Strategist Newsletter Volume 20, No. 21 on November 17, 2011.