Ends Jan 8, 2026.

By Lawrence G. McMillan
This article was originally published in The Option Strategist Newsletter Volume 17, No. 22 on November 26, 2008.
Option traders generally welcome volatile markets, for more strategies can be employed over the entire spectrum of optionable stocks. However, this market is arguably more volatile than any in history and, as such, presents a few problems and opportunities that traders might not ordinarily have considered. In this article, we’ll take a look at some of those.
In option parlance, the effects of volatility are measured by the term “vega,” which isn’t a Greek letter, but sounds like it should be. As such, it’s included with the other Greeks that describe the risk of an option. In some models and formulas, vega is called kappa, which is a Greek letter, of course. But most traders refer to the term vega to describe an option’s risk with respect to volatility. Technically it is the partial derivative of the option pricing model formula with respect to volatility.
Simplistically stated, vega is the amount by which an option’s price will change when implied volatility – expressed as an annual standard deviation (the way it normally is) – increases or decreases by one percentage point.
Example: Determining Vega by Observation:
Suppose that the following prices exist: IBM: 80 Dec 80 call: 5.10
The implied volatility of this call is 62%. If we increase implied volatility to 63%, the call’s value becomes 5.17.
Thus, by observation, the vega is 0.07 – the amount by which the call’s price increased when implied volatility increased by one percentage point.
In actual practice, one generally computes the vega of his option or of his positions by using the risk outputs from the Black-Scholes (or other) option pricing model.
Time Value Is A Misnomer
Before delving into the somewhat unique characteristics of the current market, let’s explore basic theory a little deeper. In elementary option classes, one usually learns that an option’s price is composed of “intrinsic value” and “time value.” Intrinsic value is merely the amount by which the option is in-the-money, if any. “Time Value” is the rest of the option’s price.
In reality, though, the part of the option’s price that is not intrinsic value is much more related to implied volatility than to time. If implied volatility increases, the option’s price can increase so dramatically that it might wipe out weeks, or even months, of time decay.
At the extremes, this can result in the highly unusual condition where a stock might drop, but the option’s implied volatility increases so rapidly, that an out-of-the-money call actually increases in value! This happened in the Crash of ‘87, as implied volatility of $OEX options jumped from about 20% to 150% in a week. Despite the market’s crash, deeply out-of-themoney $OEX calls actually increased in value briefly, until volatility began to decline.
Conversely, a severe decline in implied volatility can make the call price drop faster than the stock price,resulting in the seemingly illogical condition where the option’s delta appears to be greater than 1.0!
Example: XYZ is the subject of a takeover rumor, and implied volatility skyrockets from 60% to 120% because of the rumor. With the stock at 50, a one month call trades at 6.10.
The next day, however, the rumor fades and implied volatility drops to 60%. The stock falls two points on the failed rumor – to 48 – but the call drops to 2.10. Thus the call lost four points while the stock dropped two points, seemingly falling at twice the rate that the stock did. Of course, the reason was the decrease in implied volatility.
A Persistent High Volatility Market
Implied volatility ebbs and flows in all markets. This is what makes “volatility trading” viable. In some markets, the range of implied volatility for most stocks is extremely small, as in the dull bull market that took place from 2003 to 2007. During that bull market, $VIX dropped to 10 and hovered there for an inordinately long period of time, during which daily $SPX price ranges were so small that we routinely noted the historically long period of time that the index had gone without makking a daily move of 2%.
In such low-volatility markets, option selling strategies are consistent winners – although one knows that “someday” a volatility explosion could occur that will hurt such strategies. Until then, though, traders are content to sell low-priced options that generally expire worthless. Option buying is more difficult because of the relatively limited movements of the underlying stock and indices in such an environment.
The opposite is taking place now, of course, as implied volatility has exploded to unheard-of levels. Many traders are not familiar with trading in a highvolatility environment – especially one that persists for a long time as this one has been doing. Relying on methods similar to those used in a low-volatility environment will generally not work. Let’s look at one of the changes that must be made.
Adjusting Stops On Speculative Trades
In a high-volatility environment, there are a lot more “wiggles” that are meaningless to the general trend of stocks or indices. If one has a speculative position in options on these volatile instruments, he must be careful not to tighten stops too far, for he may be stopped out of a position by mere “noise” and not by a change or trend.
Recent action in the $SPX Index might serve as a prime example. We often use the 20-day moving average of the underlying as a trailing stop (although we prefer volatility-based stops). In addition, we have held various long put positions as the index has declined – particularly in the August-October, 2008 time period.
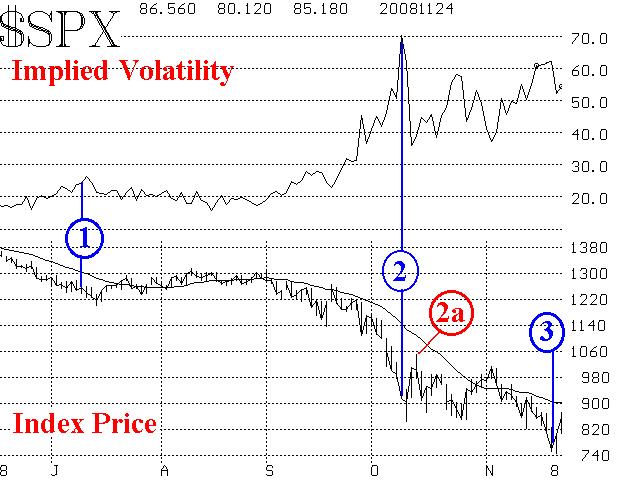
Figure 1 shows a chart of the recent action in $SPX, with a chart of the composite implied volatility of $SPX options above it. The 20-day moving average of the index price is included on the lower chart.
On the left side of Figure 1, volatility was relatively low (point “1”) and so a declining index price was trailed by a relatively nearby 20-day moving average. At that time, the trailing stop for short positions was roughly 40 $SPX points above the current $SPX price.
However, when the severity of the credit crunch began to come to light, in September and October, volatility exploded as stocks fell (point “2"). By this time, $SPX was nearly 300 points below its 20-day moving average. If one held long put positions (as we did), it would not have been appropriate to use a trailing stop on the order of magnitude of the one at point “1" (40 points or so). To illustrate, note point “2a.” There was a 200-point $SPX rally off the oversold October 10th lows, but it did not reach the 20-day moving average, nor did it stem the bearish tide, for $SPX remained in a downtrend. New lows were made by $SPX within a couple of weeks.
Thus, one had to widen the distance to the trailing stop, otherwise he would have been stopped out of his short position (or long puts) prematurely. The distance to the stop was“automatically” widened by using the 20-day moving average, but everyone doesn’t use a moving average as a stop.
A similar situation existed last week, at point “3,” with volatility still very high and $SPX 150 points below its moving average.
No matter how you are setting your stops (we encourage trailing stops), you need to widen them during volatile times. If you don’t, you will find yourself being stopped out of positions that go on to greater profits, had you merely been able to hold on longer.
Since these stops can be uncomfortably wide, we often prefer to roll profitable positions up or down, in the direction of the trend, to a) take partial profits out of the position, and b) to reduce the remaining dollars at risk.
The Effects Of Volatility On Speculative Positions
Volatility can be a help or a hindrance to a speculative position, especially during times of inflated volatility. Since volatility has never been higher than it is now, for such an extended period of time, we are seeing this effect fairly often.
Suppose you are long calls on SPY (although this would apply to any stock or index). If the index rallies, the implied volatility of those calls will likely fall (think of a falling $VIX in a rising market). Thus, your calls are hindered by the mere fact that the underlying index is rising. Of course the effect of delta (positive price change) should eventually overtake the effect of vega (implied volatility decline) if the underlying continues to rise. In the current market environment, this phenomenon is magnified since $VIX is so high and is thus sensitive to market movements (for example, when $SPX rose 110 points over two trading days, $VIX dropped 20 points).
In a similar manner, if you are long calls, but the market drops, the accompanying rise in implied volatility of a falling market will buoy the price of your calls to a certain extent – particularly in an extremely high vol market like this one. We saw this literally, in a losing position we recently had in Goldman Sachs (GS) Oct 160 calls (Position PC960). The following table summarizes the data for this trade:
| Bought | Sold | |
| Date | 8/29/08 | 9/15/08 |
| Stock Price | 164 | 157 |
| Implied Vol | 37% | 50% |
| Call Price | 10.85 | 8.15 |
Thus, even though the stock dropped 7 points over two weeks, the call only lost 2.70 because of the increase in implied volatility! Without that increase in vol, the call would have only been worth about 5.70 instead of 8.15.
We can generalize this effect: positions with positive vega are “harmed” by a rising market and “helped” by a falling market (this includes long calls and puts). Conversely, positions with negative vega are helped by a rising market and hurt by a falling market (this includes short calls and puts). Of those four types of positions – long calls, long puts, short calls, and short puts – short puts are the most responsive to a rising market (both delta and vega are helpful in a rising market), while long puts are the most responsive to a falling market (again, both delta and vega help the long puts). As a result, short puts do the worst in a falling market and long puts do the worst in a rising one. Long calls and short calls have mixed effects, because delta and vega battle against each other – in both rising and falling markets.
In summary, the effect of vega is often overlooked by traders. But in a high volatility market such as this one, the effect is larger than normal – so large that it can meaningfully affect profits and losses.
This article was originally published in The Option Strategist Newsletter Volume 17, No. 22 on November 26, 2008.
© 2023 The Option Strategist | McMillan Analysis Corporation

